Skip to main content

Jensen Shannon divergence

User Interface since version 11.0

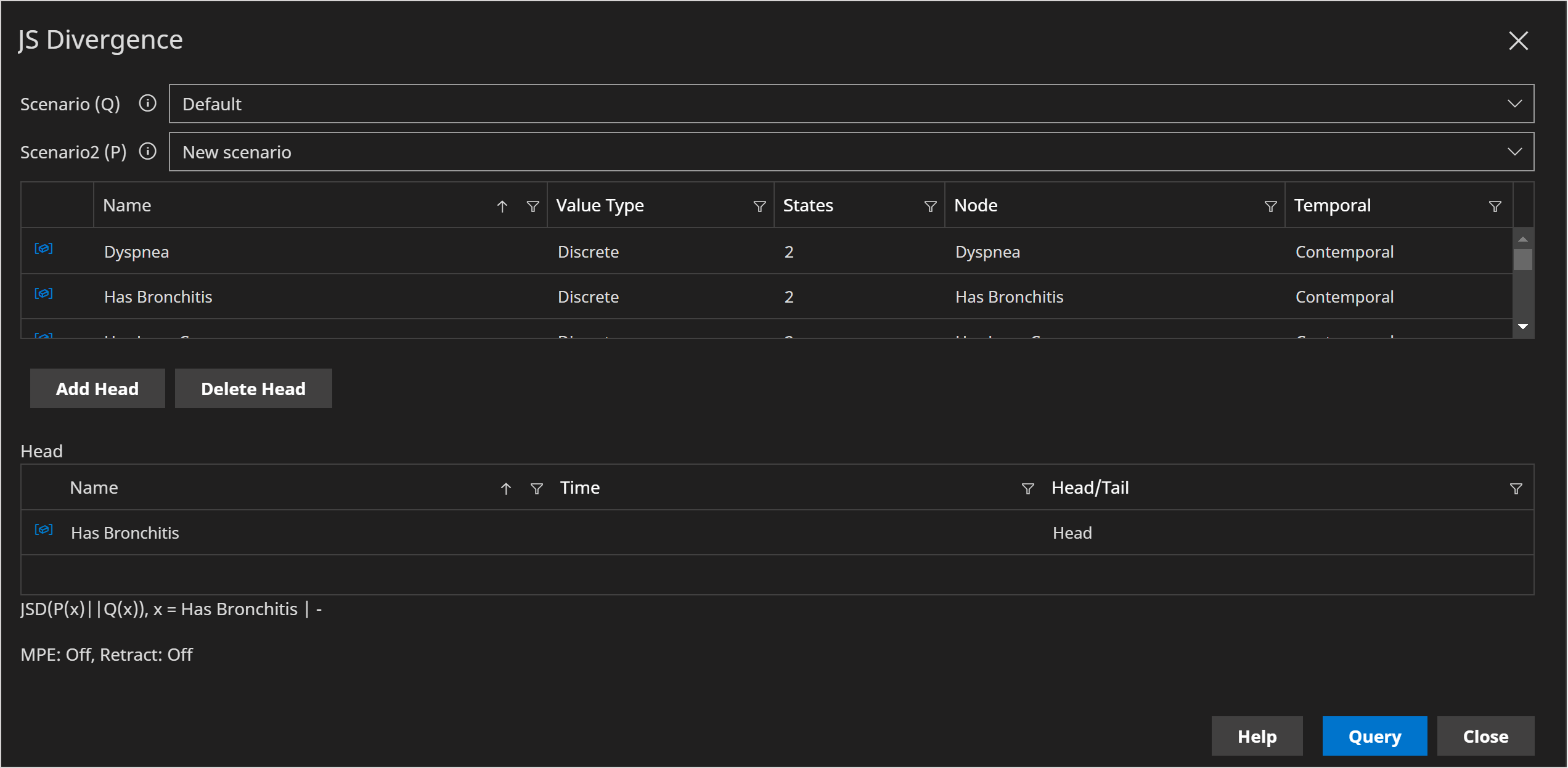
Jenson Shannon Calculator

What is Jensen-Shannon Divergence?​

The Jensen-Shannon divergence (JSD) is a powerful measure from information theory that quantifies the difference between two probability distributions. Represented as ( JSD(P || Q) ) or ( JSD(P(x) || Q(x)) ), it provides an intuitive and mathematically rigorous way to compare how one distribution differs from another.

info

The Jensen–Shannon divergence is bounded by 1 for two probability distributions, given that one uses the base 2 logarithm. 0≤JSD(P∥Q)≤10 ≤ JSD(P ∥ Q) ≤ 1

The Jenson Shannon calculator shown below supports the following:

  • One ore more discrete variables
  • One ore more continuous variables
  • Mixed discrete and continuous variables
  • Temporal variables
info

Calculations are approximate when the query contains both Discrete and Continuous variables.

Why Jensen-Shannon Divergence?​

Unlike traditional divergence measures, the JSD is both symmetrical and smoothed, making it particularly effective for real-world applications. It builds upon the Kullback–Leibler divergence by symmetrizing the measure and introducing a smoothing step to enhance stability and interpretability.

Key Features of Jensen-Shannon Divergence​

  • Symmetry: ( D(P || Q) = D(Q || P) ), ensuring fairness in comparing distributions.
  • Stability: The smoothing effect reduces sensitivity to extreme values, making it well-suited for noisy or sparse data.
  • Broad Applicability: JSD is used in machine learning, natural language processing, genomics, and more to analyze similarities or differences between datasets.

How It Works​

The JSD compares two distributions ( P(x) ) and ( Q(x) ) by first creating an average distribution ( M(x) = \frac{1}{2}(P(x) + Q(x)) ). It then measures how ( P ) and ( Q ) diverge from ( M ), providing a balanced and insightful measure of difference.