Association analysis
Since version 7.16
Association analysis evaluates the strength of relationships between sets of nodes or variables X and Y. For example, it can be used to measure the strength of links in a network. Association analysis enables modeling of dependencies. The tool helps enhance the interpretability of network structures and the interactions that drive them.
Supported for discrete, continuous, hybrid (discrete - continuous) and multi-variate nodes.
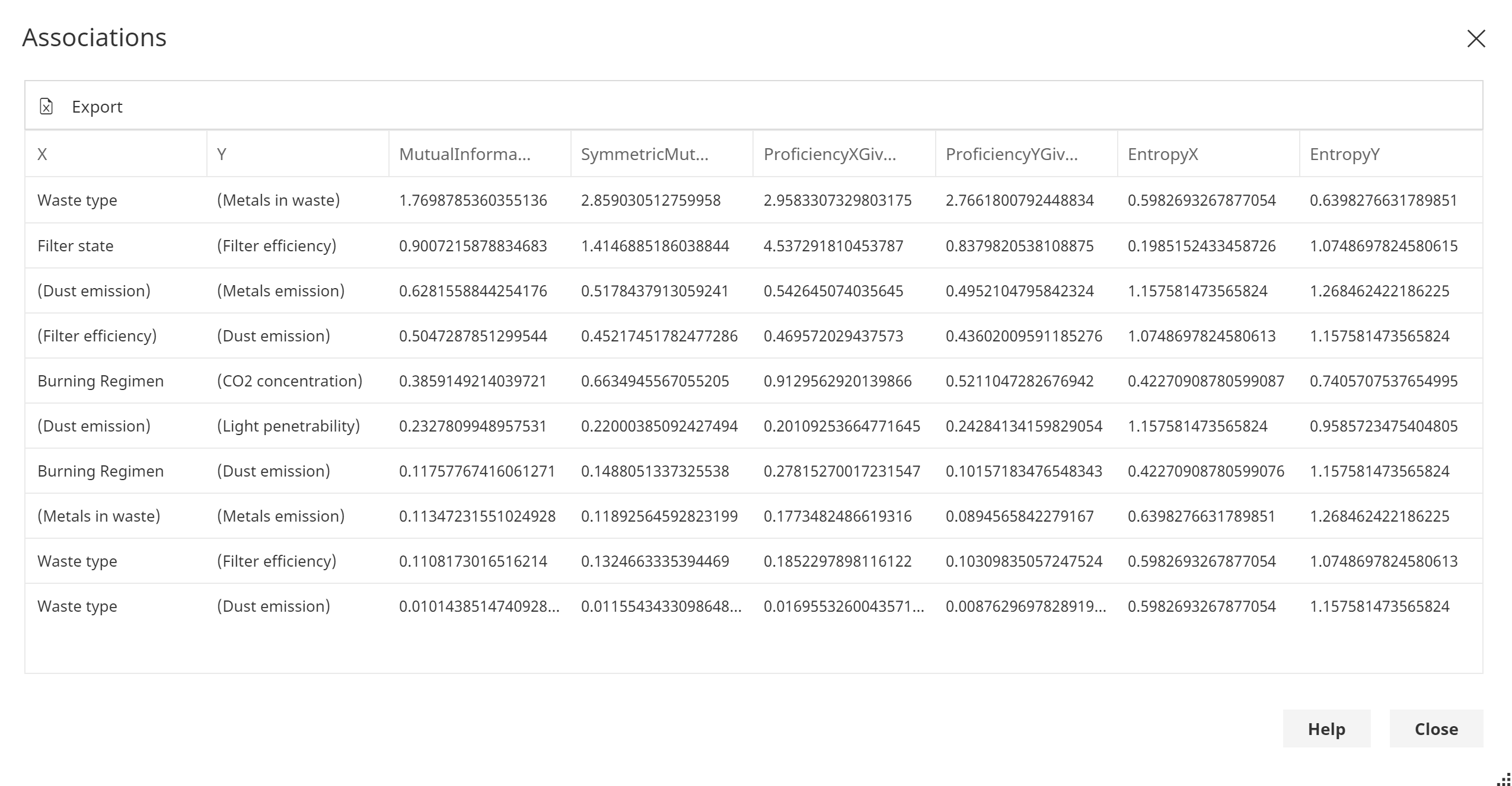
Mutual information
Mutual information quantifies the amount of information that can be gained from one variable through the other. Often denoted I(X;Y).
Entropy
The Entropy for X and Y, denoted H(X) and H(Y) respectively, are reported for convenience, as the normalized forms of the mutual information require them.
Symmetric mutual information
The symmetric mutual information (symmetric uncertainty) is a normalized version of the mutual information. It tells us the strength of the association given the level of uncertainty present in X and Y.
It equals 2 * I(X;Y) / (H(X) + H(Y))
Proficiency
The proficiency (uncertainty coefficient) normalizes the mutual information for either X or Y. For example, the proficiency of X given Y tells us how strong the relationship is given that we know Y.
The proficiency of X given Y, denoted U(X|Y) equals I(X;Y)/H(X), and
U(Y|X) equals I(X;Y)/H(Y).